


If you have other questions (like the one at the top of this post), please ask them in a comment!
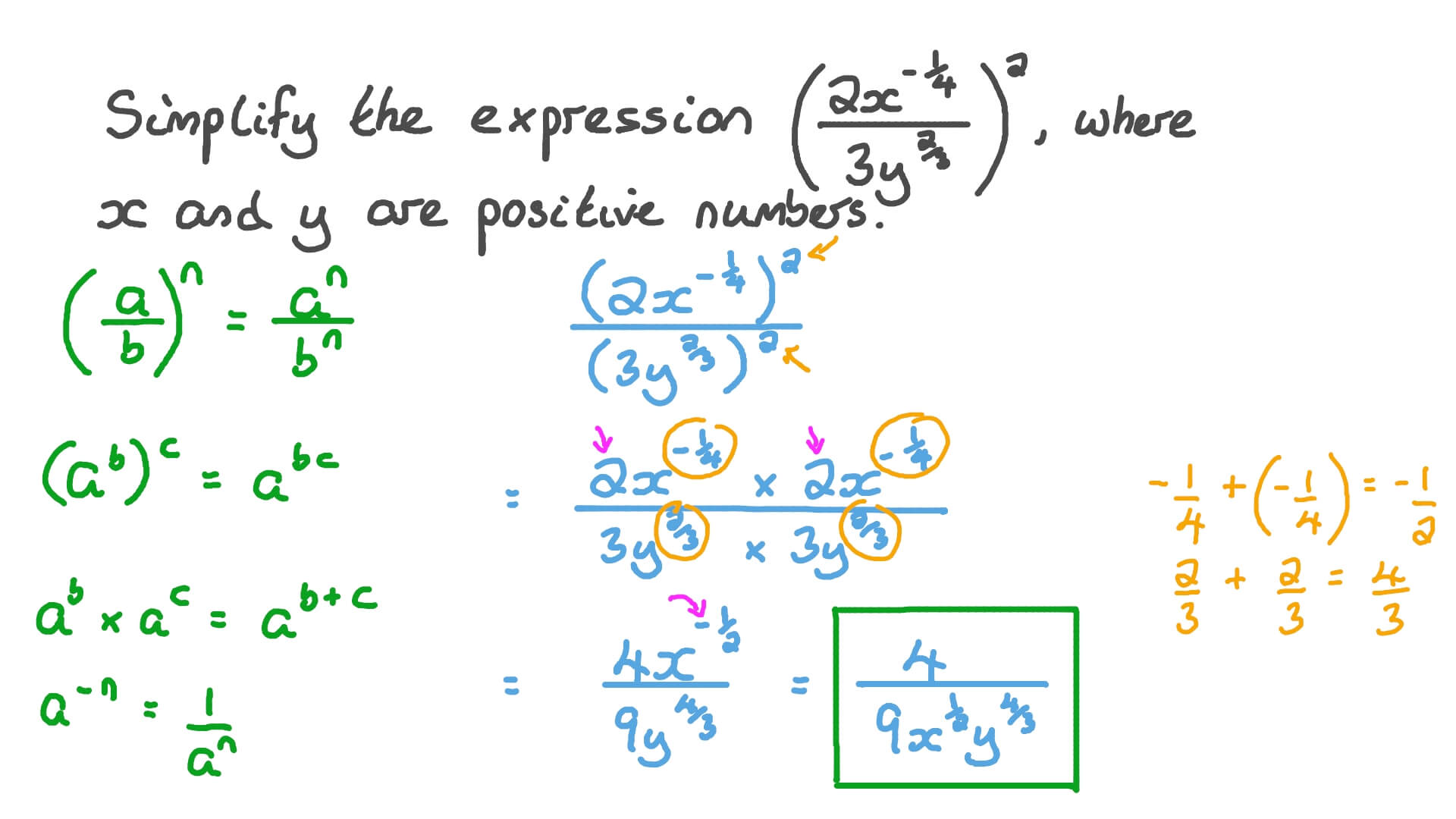
If the last step in the above two examples surprised or puzzled you, my post on Negative Differences may help clear up the confusion. So, in cases with more than one term in the numerator or denominator, the negative sign will have to be distributed if it is moved to the numerator or denominator: However, note that the negative sign must be applied to the entire numerator, or the entire denominator.
NEGATIVE EXPONENTS FRACTIONS PLUS
If there are two fractions being subtracted, and you move the subtraction sign into the numerator or denominator of the fraction being subtracted, put a plus sign where the subtraction sign was (subtracting is the same as adding a negative): As the examples above illustrate, you are welcome to move the negative sign around from where it is to either of the other two positions… whichever is most convenient for you. Summarizing these equivalent fraction results:Īs long as there is only one negative sign, either in front of the fraction, or in the numerator, or in the denominator, the fraction represents a negative quantity. We end up with the negative sign in the denominator. If we multiply the above result by 1 in the form of a negative one divided by itself to create another equivalent fraction: Recall how equivalent fractions are created: multiply the original fraction by a fraction that equals one, where numerator and denominator have the same value. Placing the negative sign before the entire fraction (subtracting the fraction) is equivalent to adding the same fraction, but with a negative numerator. These principles apply to fractions as well, so: – The negative of a number can be created by multiplying the number by negative one. – Subtraction is the same thing as the addition of a negative. Two ideas are useful to keep in mind during the explanation that follows: But where it does work, we happily use it.Question: Where should I put the negative sign when I am writing a fraction like negative two thirds?Īnswer: As long as you write only one negative sign, it does not matter where you put it. Like I mentioned above, after we use the properties to come up with a potential definition, we need to make sure it works, and it just doesn't for some types of exponents. What should $x^$ in a reasonable and unambiguous way. This brings us to your particular question.

It is a bit of work to make sure that all the other properties still hold. So if we can extend multiplication and still have the distributive property, it forces the results to be what we (now) know them to be. Thus, if we are to extend multiplication to $0$, we must have that $x*0=0$. So with multiplication, we have that $x(y+z)=xy+xz$, $xy=yx$, $x(yz)=(xy)z$, and $1*x=x*1=x$, and the question is, can we extend multiplication to negative/rational/real/complex numbers while maintaining these properties? What mathematicians have found is that one should look for properties that hold in the familiar case, declare that any reasonable extension will still have these properties, and use these properties to define what happens in the unfamiliar case. But in this case, what is $m*n$ when $m$ is not a positive integer? Or when neither $m$ nor $n$ are?Īt this point, these expressions don't have any meaning, and you have to decide how you want to give them meaning. If you write $n*m=m+m+\ldots +m$ where you have added $m$ to itself $n$ times, then you can extend the formula to when $m$ is not a positive integer. There are obvious real world ways to give meaning to these expressions in terms of counting of objects when the operations involve positive integers. When you are starting out with arithmetic, first you have counting, then you have addition of positive numbers, and then you have repeated addition, which is multiplication.


 0 kommentar(er)
0 kommentar(er)
